Complex Rotations Extra Challenge 2
\[cos(\theta)=\frac{e^{i\theta}+e^{-i \theta}}{2}\] \[sin(\theta)=\frac{e^{i\theta}-e^{-i \theta}}{2i}\]
Before we break down these formulas we should make sure we understand complex conjugates well. As stated in the main post, we define the conjugate of a complex number \(z=a+bi\) as \(\bar{z}=a-bi\).
So let \(z=e^{it}\) be a generic complex number with radius 1 and angle \(t\). Here I’ve labeled \(\bar{z}\) as \(z\_c\):
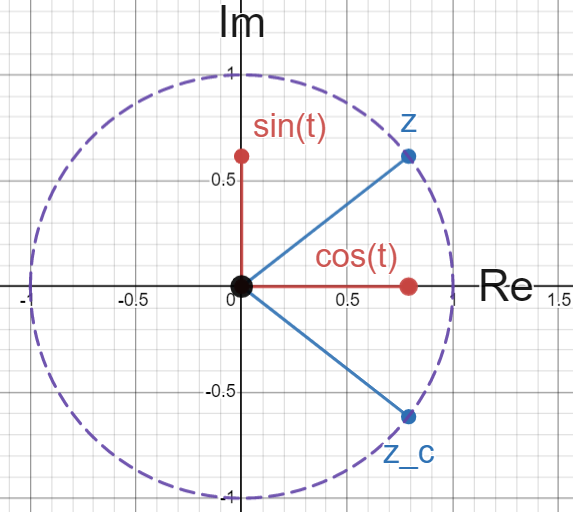
The real and imaginary components of \(z\) have also been shown in red. It should be noted that \(z\) can be “reflected up” and doesn’t have to start with a positive imaginary (or real) component.
You’ll notice from this image that \(\theta_{\bar{z}} = - \theta_{z}\), which means when we have these formulas,
\[cos(\theta)=\frac{e^{i\theta}+e^{-i \theta}}{2}\] \[sin(\theta)=\frac{e^{i\theta}-e^{-i \theta}}{2i}\]
You can look at them like this!
\[cos(\theta_{z})=\frac{z+\bar{z}}{2}\] \[sin(\theta_{z})=\frac{z-\bar{z}}{2i}\]
This is a much easier way to envision what this formula is actually telling us to do.
So let’s see what happens when we add together \(z\) and \(\bar{z}\) as the first formula suggests we do.
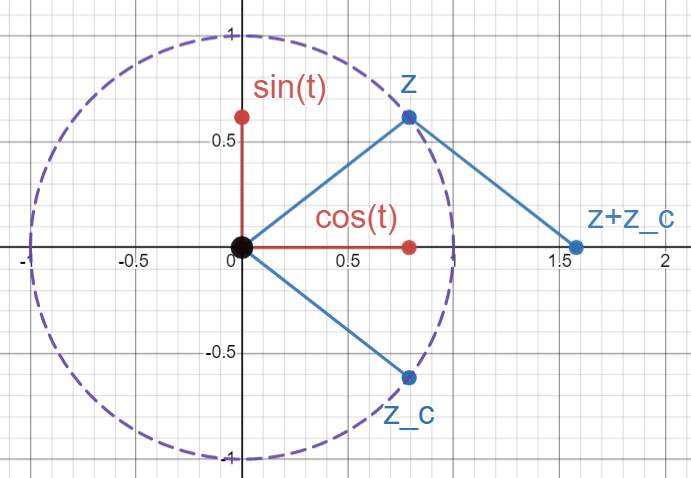
Since \(z\) and \(\bar{z}\) both have the same real component, we see that the real component for \(z + \bar{z}\) is twice \(cos(t)\). So this means to get back to \(cos(t)\) we just have to take \(z + \bar{z}\) and divide by 2! This is such a simple way to visualize the path that this complicated looking formula takes us on.
We can do a similar thing with the second formula, but there’s a small catch. When we talk about \(sin(t)\) like it’s shown in the diagram, we mean strictly the length of that red bar, not its location. The \(sin\) function outputs a real number and has no encoding of real vs imaginary components, this is why we have \(i \space sin(\theta)\) in Euler’s Formula. However, the actual value of \(z\) and \(\bar{z}\) do encode both real and imaginary components.
With this in mind, lets follow where the formula takes us:
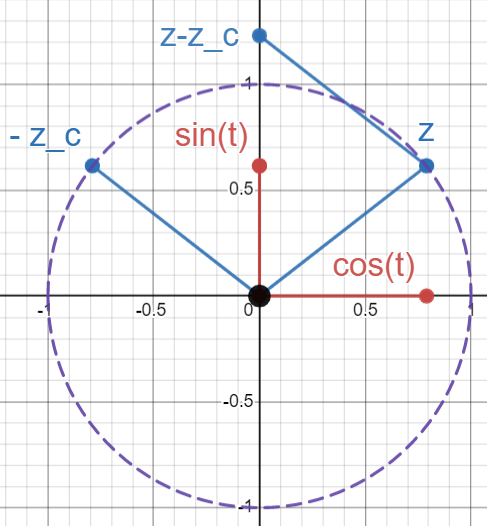
Similar to before, we find ourselves at the location double the distance along the imaginary axis from \(i \space sin(t)\). To get to this location we must first divide by 2. Here’s where the above note comes into play. We are ultimately looking for \(sin(t)\), but right now we find ourselves at \(i \space sin(t)\), so we must divide by \(i\). Putting all the steps together we get \(sin(t) = \frac{z-\bar{z}}{2i}\), what we were trying to conclude!
Side Challenge: Try to convince yourself both algebraically and visually why we can either say “divide by \(i\)” or “multiply by \(-i\)”.
Click here to return to the post.
Click here to return home.