Complex Rotations Extra Challenge 1

---

Evaluate \(z=\sqrt{4(\frac{1}{2}+i\frac{\sqrt{3}}{2})}\)

Scroll Down to just see the answer.

---

This challenge combines ideas mentioned in the last 2 problems of the main post. In the same way where, in Problem 3 we were looking for a \(z\) such that \(z^{2} = i\), here we’re looking for a \(z\) such that \(z^{2}=4(\frac{1}{2}+i\frac{\sqrt{3}}{2})\)

So lets take a look at where this point lies, lets call it point \(p\):

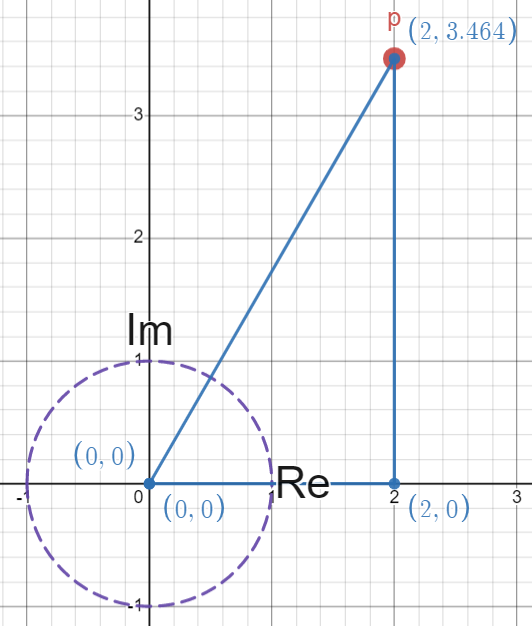
Using the pythagorean theorem we can see that the radius of this value is 4. Some might also have noticed that \(\frac{1}{2}+i\frac{\sqrt{3}}{2}\) lies on the complex unit circle, meaning it has radius 1, which is then scaled by 4.

To find the angle that \(p\) lies at, we can use some trigonometry, although many of you might have known the value of this angle by memory.

\(\theta_{p} = tan^{-1}(\frac{\sqrt{3}}{2}/{\frac{1}{2}}) = tan^{-1}(\sqrt{3}) = \frac{\pi}{3}\)

So now that we have the angle and radius of \(p\) we can find those values for \(z\):

Multiplying \(z\) by itself doubles its angle, so we need \(2\theta_{z} = \theta_{p} \implies \theta_{z} = \frac{\pi}{6}\)

Also, multiplying \(z\) by itself will square its radius, so we need the length of \(z\) to be the sqaure root of the length of \(p\), namely \(\pm 2\)

So there’s our solution!

\[z = \pm 2 e^{i\frac{\pi}{6}}\]

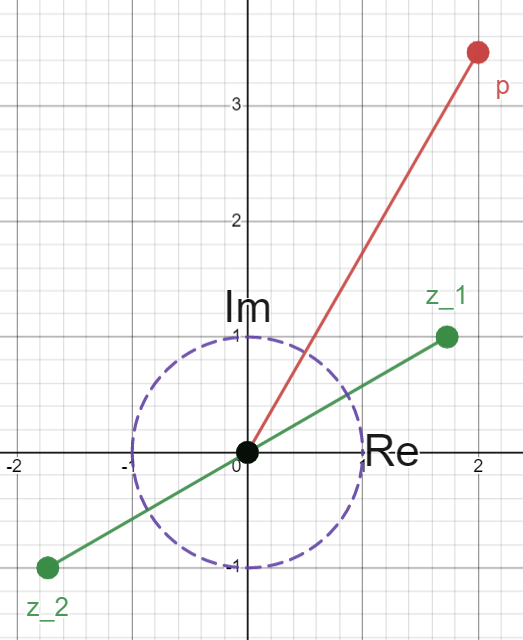
Notice how each of these have a smaller radius than \(p\) and are halfway in angle to \(p\) from the positive real axis.

---

Answer

\(z=\sqrt{4(\frac{1}{2}+i\frac{\sqrt{3}}{2})}\)

\(z = \pm 2 e^{i\frac{\pi}{6}}\)

---

Click here to return to the post.

Click here to return home.